FWH: Support for Matrix calculations
Posted: Thu Dec 10, 2020 8:31 pm
In the coming version, FWH provides an easy interface to perform complex matrix calculations with its new class FW_Matrix.
Using this class, matrix calculations can be as simple as performing normal arithmetic like this:
matrix3 is an FW_Matrix() object obtained by matrix multiplication of matrix1 and matrix2, which are FW_Matrix() objects.
Same way to get Inverse of a matrix
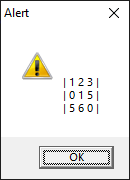
A simple way to view a matrx object:
While we can use corresponding methods of the class, in many cases using operators like above makes is much easier.
Example:
In the above code, all variables are FW_Matrix objects.
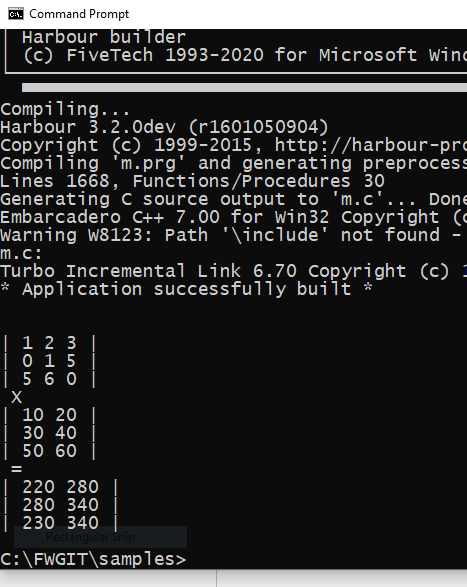
This is a simple sample program:
fwh\samples\matrix01.prg:
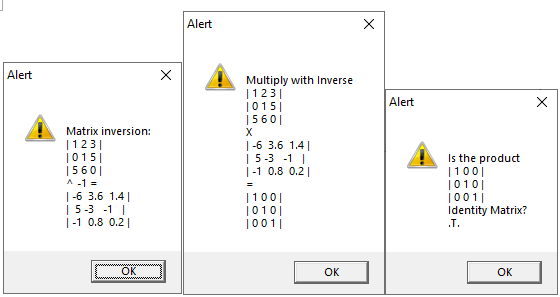
In the above sample, these lines of code:
produce this result:
These lines of code:
produce this result:
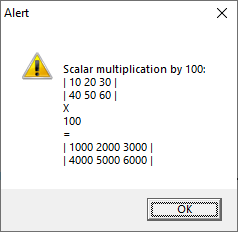
This last line of code:
produces this result:
Detailed documentation of the class FW_Matrix follows. In this class, all computations are performed in Harbour code. Though this is quite fast enough mostly, there can be more demanding applications that need complex matrix calculations performed in large loops. To support this, highly optimized C level functions are also provided.
Using this class, matrix calculations can be as simple as performing normal arithmetic like this:
Code: Select all
matrix3 := matrix1 * matrix2
Same way to get Inverse of a matrix
Code: Select all
matrix_inverse := matrix1 ^ -1
Code: Select all
? oMatrix

While we can use corresponding methods of the class, in many cases using operators like above makes is much easier.
Example:
Code: Select all
output := ( training_set_inputs * synaptic_weights ):Sigmoid()
synaptic_weights += ( training_set_inputs:Transpose() * ( training_set_outputs - output ) * output * output:Calc( { |x| 1 - x } ) )
This is a simple sample program:
fwh\samples\matrix01.prg:
Code: Select all
#include "fivewin.ch"
#xtranslate matrix( <a> ) => FW_Matrix():New( <a> )
//----------------------------------------------------------------------------//
function Main()
local M1, M2, M3, M4
M1 := matrix( { { 1, 2, 3 }, { 0, 1, 5 }, { 5, 6, 0 } } )
? "Matrix inversion:", M1, "^ -1 =", M2 := M1 ^ -1
? "Multiply with Inverse", M1, "X", M2, "=", M3 := M1 * M2
? "Is the product", M3, "Identity Matrix?", M3 == 1
M2 := matrix( { { 10,20, 30 }, { 40, 50, 60 } } )
? "Another matrix multiplication", M2, "X", M1, "=", M3 := M2 * M1
? "Check by dividing matrices", M3, "/", M1, "=", M4 := M3/M1
? "Is result correct?", M4, "==", M2, "=", M4 == M2
? "Scalar multiplication by 100:", M2, "X", 100, "=", M2 * 100
return nil
//----------------------------------------------------------------------------//
Code: Select all
M1 := matrix( { { 1, 2, 3 }, { 0, 1, 5 }, { 5, 6, 0 } } )
? "Matrix inversion:", M1, "^ -1 =", M2 := M1 ^ -1
? "Multiply with Inverse", M1, "X", M2, "=", M3 := M1 * M2
? "Is the product", M3, "Identity Matrix?", M3 == 1

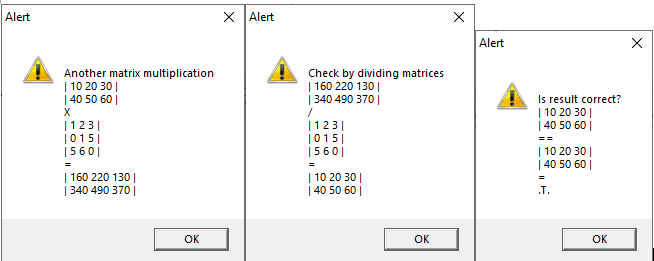
These lines of code:
Code: Select all
M2 := matrix( { { 10,20, 30 }, { 40, 50, 60 } } )
? "Another matrix multiplication", M2, "X", M1, "=", M3 := M2 * M1
? "Check by dividing matrices", M3, "/", M1, "=", M4 := M3/M1
? "Is result correct?", M4, "==", M2, "=", M4 == M2

This last line of code:
Code: Select all
? "Scalar multiplication by 100:", M2, "X", 100, "=", M2 * 100

Detailed documentation of the class FW_Matrix follows. In this class, all computations are performed in Harbour code. Though this is quite fast enough mostly, there can be more demanding applications that need complex matrix calculations performed in large loops. To support this, highly optimized C level functions are also provided.